O que é criptografia ?

Criptografia (do grego: kryptós, “escondido”, e gráphein, “escrita”)é uma técnica utilizada para proteger informações e garantir sua confidencialidade, integridade e autenticidade durante a transmissão ou armazenamento. Consiste em converter os dados originais (texto, arquivos, etc.) em um formato ilegível, chamado de texto cifrado ou criptograma, por meio de algoritmos matemáticos e chaves de criptografia. Assim, pessoas não autorizadas ou terceiros que, por qualquer motivo, tenham acesso as informações, elas estarão ilegíveis, assim tornando-as inúteis.

O processo de criptografia envolve a aplicação de um algoritmo específico, que realiza operações matemáticas nos dados originais, combinando-os, ou não, com uma chave de criptografia. Essa chave é uma sequência de caracteres ou valores numéricos que determina como os dados serão cifrados. A mesma chave é necessária para reverter o processo de criptografia, para assim, obter os dados originais.

Existem dois tipos primarios de criptografia, incluindo a criptografia simétrica e a criptografia de chave pública (assimétrica). Na criptografia simétrica, a mesma chave, ou o mesmo método é usado tanto para criptografar quanto para descriptografar os dados. Já na criptografia de chave pública, são utilizadas duas chaves diferentes: uma chave pública, que é compartilhada e usada para criptografar os dados, e uma chave privada, mantida em sigilo pelo destinatário, que é usada para descriptografar os dado, esse segundo modelo é amplamente usado nos dias de hoje para as comunicações de dados digitalmente.

A criptografia desempenha um papel fundamental em diversos campos, como comunicações seguras, proteção de dados pessoais, transações financeiras online, segurança da informação e muitos outros. Ela permite que as informações permaneçam confidenciais, mesmo se forem interceptadas por terceiros não autorizados, fornecendo uma camada adicional de segurança e privacidade. Nesse trabalho vamos entender alguns métodos, estudar sua historia e fazer uma analise matemática.

A cifra de Cesar

Quando falamos em criptografia logo pensamos em algo mais atual, isso se dá talvez ao uso extensivo dessa palavra no meio digital, mas não se engane, a criptografia não é algo exclusivo da época moderna. A cifra de Cesar por exemplo é uma cifra muito famosa, até nos dias de hoje, esta cifra foi nomeada através de Júlio César, o general Romano que foi o principal responsável por transformar Roma em um império aproximadamente em 50 a.C. Essa cifra, classificada como uma Cifra de Substituição, consistia em substituir cada letra da mensagem pela letra três posições depois dela.

Sua Historia

A Cifra de César é uma técnica de criptografia histórica que recebeu esse nome em referência ao imperador romano Júlio César, general do império romano aproximadamente em 50 a.C., que supostamente a teria utilizado para proteger suas comunicações militares. Embora não haja evidências históricas concretas de que César tenha usado essa cifra, ela é amplamente associada a ele devido à sua popularidade e simplicidade. Embora a cifra de César seja popularmente associada ao imperador romano Júlio César, não há evidências históricas sólidas de que ele a tenha utilizado. No entanto, a técnica de substituição alfabética que ficou conhecida como cifra de César era amplamente usada na antiguidade e é possível que tenha sido empregada por vários governantes e líderes militares da época.

Embora a cifra de César seja considerada muito fraca pelos padrões modernos de criptografia, ela foi uma técnica eficaz em sua época. A maioria das pessoas naquela época não era alfabetizada, e aqueles que eram, provavelmente não conheciam a cifra de César nem possuíam os recursos necessários para quebrá-la facilmente. Hoje em dia, a cifra de César é mais conhecida por seu uso como exemplo de criptografia básica e como uma introdução ao estudo de cifras mais complexas. Ela ilustra os princípios básicos da criptografia por substituição e a importância de chaves secretas na proteção das informações.

Como a cifra funciona

A cifra de César é um exemplo de cifra de substituição, em que cada letra do alfabeto é substituída por outra letra, geralmente a uma posição fixa adiante no alfabeto. Por exemplo, com um deslocamento de três posições, a letra “A” seria substituída por “D”. A criptografia usando a cifra de César é relativamente simples. O remetente e o destinatário devem concordar com um valor fixo de deslocamento, conhecido como chave. O remetente então substitui cada letra da mensagem original pela letra correspondente no alfabeto deslocada pela quantidade especificada pela chave. Por exemplo, se a chave for 3, a palavra “OLA” seria cifrada como “ROD”.

![[cesar.png|center|500]]
Diagrama Cifra de Cesar

Essa cifra é considerada uma das mais básicas e facilmente quebráveis, pois há apenas 25 possibilidades de deslocamento (já que o deslocamento de 0 ou 26 resulta na mesma mensagem original). A criptoanálise da cifra de César é simples, pois pode-se testar todas as 25 opções possíveis para encontrar a mensagem original.

Embora a cifra de César seja uma técnica bastante simples, ela serviu como base para o desenvolvimento de outras cifras mais complexas ao longo da história. Além disso, a ideia de cifrar mensagens através da substituição de letras no alfabeto é fundamental para a compreensão de princípios criptográficos mais avançados. Apesar de sua aparente falta de segurança, a cifra de César ainda é utilizada como um exemplo didático para ensinar os princípios básicos da criptografia e para ilustrar a importância da segurança das informações.

Exemplo

Vamos ver alguns exemplos de como a cifra funciona. Vamos tomar a seguinte frase “A ligeira raposa marrom saltou sobre o cachorro cansado” vamos fazer uma rotação de chave 3, ou seja, vamos mudar a letra “A” pela letra “D”, “B” por “E”, e assim por diante, teremos o seguinte:

Texto plano: A ligeira raposa marrom saltou sobre o cachorro cansado
Texto cifrado: D OLJHLUD UDSRVD PDUURP VDOWRX VREUH R FDFKRUUR FDQVDGR

Podemos ver que de fato é uma cifra simples, e que pode ser facilmente usada por qualquer um que saiba o alfabeto. Porem, não podemos deixar essa simplicidade nos enganar, em uma analise mais profunda iremos perceber que essa cifra esconde uma certa complexidade em sua simplicidade.

Analise Matemática da cifra de Cesar

Vamos agora escrever um algoritimo para a cifra de Cesar em linguagem matemática.
Vamos tomar \(k\) como a chave, \(p\) como a letra a ser encriptada e \(c\) como a letra criptografada. As variáveis \(p\) e \(c\) são usadas para representar a letra que está sendo criptografada porque na criptografia nos referimos à mensagem original como ‘texto simples’ e à mensagem criptografada como ‘texto cifrado’.
Sabemos que \(k\), representa um número porque é a chave. Mas \(p\) e \(c\) são na verdade letras. Precisamos convertê-los em números. Isso é muito simples. Represente “A” por 0, “B” por 1, “C” por 2… “Z” por 25.
Ao criptografar uma mensagem, estamos deslocando-a em $k$ letras. Em termos de números, estamos apenas adicionando \(k\) a \(p\) para obter \(c\). Logo podemos usar o seguinte equação para obter \(c\):
$$c=p+k$$
Porem, com esse método temos um problema, vamos tomar um \(k=1\) e a letra “Z”, sabemos que o p que representa a letra “Z” é 25, logo temos um \(c=26\), porem 26 não nos leva até uma letra do alfabeto, seguindo a regra previamente estabelecida. Esse problema ocorre devido ao ‘enrolamento’ de “Z” para “A”. Para corrigir isso, podemos usar a aritmética modular. Estaremos quase sempre trabalhando no mod 26 porque existem 26 letras no alfabeto. Nossa nova equação seria:
$$c \equiv p+k \;(mod\;26)$$
Vamos fazer alguns testes dessa pequena equação, vamos tomar novamente \(k=1\) e a letra “Z”, ou seja \(p=25\), nesse caso temos:
$$c \equiv 25+1\;(mod\;26)$$
$$c \equiv 26\;(mod\;26)$$
Na operação modulo temos o resultado como o resto da divisão, nesse caso, temos o resto da divisão de \(26\) por \(26\), sendo assim \(0\), logo temos que \(c=0\) exatamente o que precisávamos.
Podemos ainda criar uma equação semelhante para descriptografar o texto cifrado:
$$p \equiv c-k\;(mod\;26)$$
Vamos tomar o exemplo anterior para verificar essa equação, sabemos que \(c=0\) e \(k=1\), assim teremos:
$$p\equiv0-1\;(mod\;26)$$
$$p\equiv-1\;(mod\;26)$$
$$p=25$$
Exatamente com o que começamos.

Uma aplicação dentro da programação

Podemos ainda criar um algoritimo muito simples para a cifra de Cesar para nos retornar o texto cifrado, então como curiosidade, deixo a seguir uma possivel aplicação desse algoritimo:

def cesar(input_text,key):
    output = ""
    input_text = input_text.upper() #Convertendo a entrada em maiusculo
    for letter in input_text:#interando para cada letra da entrada
        output += chr(int((key + (ord(letter)-65)) % 26)+65)#ASCII
    return output

text = input("Digite a frase a ser cifrada: ")
key = input("Digite a chave: ")
key = int(key)
print(cesar(text,key))

Note que estamos usando exatamente a equação que desenvolvemos previamente. Mais a frente na historia, uma processo de criptografia semelhante foi usado pelos nazistas durante a segunda guerra, eles construiram uma maquina complexa, que usava a ideia da criptografia de Cesar, mas como diversos passos extras, eles chamaram essa maquina de Enigma.

A maquina enigma

Durante a Segunda Guerra Mundial, a máquina Enigma foi uma das mais sofisticadas e avançadas tecnologias de criptografia utilizadas pelas forças alemãs, especialmente pela marinha, exército e força aérea. A Enigma foi desenvolvida na década de 1920 e era um sistema eletromecânico de cifragem que permitia aos alemães codificar suas mensagens de forma segura. Acredita-se que a máquina tenha sido usada em grande parte do conflito, tornando-se um dos principais desafios de criptoanálise enfrentados pelos Aliados.

O funcionamento da máquina Enigma era baseado em uma série de rotores que giravam para cada caractere digitado, produzindo uma sequência aparentemente aleatória de letras como saída. O processo de codificação era altamente complexo e, para decifrar as mensagens, os destinatários precisavam ter conhecimento prévio das configurações dos rotores e das posições iniciais. A matemática desempenhou um papel fundamental na quebra dos códigos da Enigma pelos Aliados. A tarefa de quebrar o código era extremamente difícil devido ao grande número de combinações possíveis de configurações dos rotores e das chaves diárias. No entanto, um grupo de matemáticos, criptógrafos e cientistas, notavelmente reunidos no Bletchley Park, no Reino Unido, trabalhou incansavelmente para decifrar as mensagens codificadas.

Um dos matemáticos mais importantes envolvidos nesse esforço foi Alan Turing, cujo trabalho foi fundamental para a quebra dos códigos da Enigma. Turing desenvolveu uma máquina chamada “Bombe”, que tinha a capacidade de testar rapidamente várias configurações possíveis dos rotores e chaves diárias da Enigma. A Bombe reduzia drasticamente o tempo necessário para encontrar as configurações corretas e, assim, possibilitava a decodificação das mensagens inimigas de maneira mais eficiente.

A matemática usada para quebrar o código da Enigma envolvia análises estatísticas, teoria dos números e conceitos de combinatória. Além disso, a equipe de Bletchley Park contava com uma grande quantidade de dados interceptados, o que possibilitava a aplicação de métodos de criptoanálise para identificar padrões nas mensagens codificadas e, consequentemente, encontrar as configurações corretas da máquina Enigma.

O trabalho de decifrar os códigos da Enigma foi altamente secreto e considerado uma das mais bem-sucedidas operações de inteligência da Segunda Guerra Mundial. A habilidade de ler as comunicações inimigas permitiu que os Aliados soubessem antecipadamente dos movimentos das forças alemãs, dando-lhes uma vantagem estratégica significativa em várias batalhas e contribuindo para a vitória final na guerra. A quebra dos códigos da Enigma pelos Aliados foi um marco importante no desenvolvimento da criptoanálise e das ciências da computação. Além de sua relevância histórica, esse episódio demonstrou a importância da matemática e do pensamento lógico na resolução de problemas complexos relacionados à segurança da informação.

Alan Turing

Alan Turing nasceu em Paddington, Londres, em 23 de junho de 1912. Seu pai, Julius Mathison Turing, era um membro britânico do Serviço Civil Indiano e estava frequentemente no exterior, enquanto sua mãe, Ethel Sara Stoney, era filha do engenheiro-chefe das ferrovias de Madras. Quando Alan tinha cerca de um ano de idade, sua mãe voltou para a Índia para se reunir com seu marido, deixando Alan na Inglaterra sob os cuidados de amigos da família. Ele frequentou a escola, mas não parecia estar se beneficiando, então foi retirado após alguns meses.

Em seguida, ele foi enviado para a Escola Preparatória de Hazlehurst, onde parecia ser um aluno “médio a bom” na maioria das matérias, mas estava muito envolvido em seguir suas próprias ideias. Ele se interessou por xadrez enquanto estava nessa escola e também se juntou à sociedade de debates. Alan concluiu seu Exame de Entrada Comum em 1926 e depois foi para a Escola Sherborne. Ele encontrou dificuldades para se encaixar no que era esperado nessa escola pública, mas seu gênio o impulsionava em suas próprias direções, em vez daquelas exigidas por seus professores.

Turing foi criticado por sua caligrafia, teve dificuldades em inglês e, mesmo em matemática, estava muito interessado em suas próprias ideias para produzir soluções para problemas usando os métodos ensinados por seus professores. Apesar de fornecer respostas não convencionais, Turing ganhou quase todos os prêmios de matemática possíveis enquanto estava em Sherborne. Em química, um assunto que o interessava desde muito jovem, ele realizou experimentos seguindo sua própria agenda, o que não agradou seu professor. O diretor de Turing escreveu: “Se ele permanecer na escola pública, deve aspirar a se educar. Se ele for apenas um especialista científico, está desperdiçando seu tempo na escola pública”.

Apesar dos anos difíceis na escola, Turing ingressou no King’s College, Cambridge, em 1931 para estudar matemática. Ele leu os trabalhos de Einstein sobre relatividade e também leu sobre mecânica quântica no livro de Eddington, “A natureza do mundo físico”. Em 1933, Turing começou a se interessar pela lógica matemática e apresentou um trabalho ao Moral Science Club de Cambridge sobre a interpretação lógica das proposições matemáticas.

Após concluir seus estudos em Cambridge, Turing foi eleito membro do King’s College em 1935 e escreveu uma dissertação sobre a função de erro gaussiana, que estabeleceu resultados fundamentais em teoria das probabilidades, como o teorema do limite central. Em 1936, ele publicou o artigo “Sobre números computáveis, com uma aplicação ao problema da decisão”, onde introduziu a máquina abstrata chamada “máquina de Turing”, que se tornou um conceito fundamental para a ciência da computação.

Com o início da Segunda Guerra Mundial em 1939, Turing se juntou ao Government Code and Cypher School em Bletchley Park, onde desempenhou um papel crucial na quebra dos códigos da máquina Enigma alemã. Ele foi um dos principais responsáveis pelo desenvolvimento da máquina chamada “Bombe”, que decifrava as mensagens Enigma. O trabalho realizado em Bletchley Park salvou inúmeras vidas durante a guerra.

Após a guerra, Turing foi convidado pelo National Physical Laboratory em Londres para projetar um computador. Ele apresentou um relatório propondo o Automatic Computing Engine (ACE) em 1946. Turing também continuou suas pesquisas em áreas como morfogênese e teoria quântica. No entanto, em 1952, ele foi preso por violação das leis britânicas de homossexualidade.

Após sua condenação, Turing foi submetido a tratamentos hormonais com estrogênio e teve sua autorização de segurança revogada. Ele continuou seu trabalho acadêmico, mas sofreu com problemas pessoais e restrições devido ao seu status de segurança. Em 1954, Turing morreu devido a envenenamento por cianeto de potássio, em um incidente considerado suicídio, embora sua mãe tenha afirmado que tenha sido um acidente.

Alan Turing foi um pioneiro na teoria da computação e suas contribuições tiveram um impacto duradouro no campo da ciência da computação. Sua genialidade e trabalho pioneiro na quebra dos códigos de Enigma durante a Segunda Guerra Mundial foram fundamentais para a vitória dos Aliados. Apesar das dificuldades pessoais que enfrentou e das circunstâncias trágicas de sua morte, o legado de Turing continua sendo uma fonte de inspiração para a ciência e a tecnologia.

A maquina Enigma

Enigma com a caixa de rotores aberta

A Máquina Enigma consistia em uma série de rotores, um teclado e um painel de luzes indicadoras. O operador começava selecionando uma configuração inicial para os rotores. Os rotores tinham contatos elétricos internos e podiam ser posicionados de várias maneiras, criando um vasto número de combinações possíveis. Quando uma letra era pressionada no teclado, um circuito elétrico era estabelecido entre o contato do rotor que representava essa letra e outro contato correspondente no painel de luzes. O primeiro rotor girava um passo após cada pressionamento de tecla, mudando o mapeamento de letras e criando uma substituição diferente para cada letra pressionada. O segundo rotor girava após cada revolução completa do primeiro rotor e assim por diante, proporcionando um alto nível de complexidade ao processo de codificação. Após a letra ser substituída por outra letra na primeira passagem pelos rotores, o sinal passava por um conjunto de fios conectados a um refletor. O refletor, por sua vez, enviava o sinal de volta através dos rotores, resultando em uma letra final codificada, que era então iluminada no painel de luzes. A letra final era a mensagem criptografada que podia ser transmitida de forma segura.

Como vimos com a cifra de Cesar cada letra de um texto original terá uma correspondente unica no texto cifrado, a maquina Enigma faz um processo semlehante a cifra de cesar, tranformando um textode entrada em um texto de saida com as letras embaralhadas, porem devido a presença dos rotores, uma mesma letra no texto original pode não ter uma mesma equivalente no texto cifrado, vamos ver uma exemplo:

Texto original: A ligeira raposa marrom saltou sobre o cachorro cansado
Cifra de Cesar(chave 3): D OLJHLUD UDSRVD PDUURP VDOWRX VREUH R FDFKRUUR FDQVDGR
Enigma: p vpernnj tfztqx auuapv qstakz iavys b ougvcyaa hcganyq

Perceba que para uma mesma letra, como por exemplo a letra “A” no texto cifrado com a cifra de Cesar, tem sempre uma mesma letra correspondente, nesse caso a letra “D”, porem no texto cifrado pelo Enigma, temos que a letra “A” no texto original possui letras correspondentes diferentes. Dessa forma, durante a segunda guerra, os nazistas estavam certos de que eles possuíam uma cifra inquebrável, mas como eles poderiam ter tanta certeza ?

A matemática na maquina enigma

Sabemos que a maquina Enigma precisava de $3$ rotores para funcionar, cada um deles rotacionam para cada tecla pressionada, assim mudando a letra de saída para algo pré-programado no rotor, ao todo, junto da Enigma, haviam $5$ rotores diferentes para serem escolhidos, todos diferentes entre si, assim podemos calcular quantas possibilidades de rotores podemos arrumar dentro da Enigma, vamos chamar essa quantidade de arranjos de $r$:
$$r=5\times4\times3=60$$
Porem cada rotor possuíam um total de 26 possibilidades de posições iniciais, assim, podemos calcular o total de posições inicias de cada rotor, vamos chamar essa quantidade de $r_s$:
$$r_s=26\times26\times26=17576$$

A maquina enigma possuía duas versões dentro da Alemanha, uma versão comercial e outra versão militar, em especial, a versão militar tinha uma funcionalidade extra, algo chamado de plugboard.

Enigma plugboard

Ao todo se tinham 10 fios, e esses fios conectavam um par de letras dispostos na frente da maquina, quando duas letras estavam conectadas por um desses fios, elas seriam trocadas no texto cifrado, assim, podemos calcular o total de arranjos para as letras, vamos chamar esse total de arranjos de $p$:
$$p=\frac{26!}{10!\;6!\;2^{10}}$$
$$p=150.738.274.937.250$$

Assim temos um total de combinações $T$:
$$T=p \times r_s \times r$$
$$T=158.962.555.217.826.360.000$$

Note que, para todas as mensagens cifradas possíveis geradas pela maquina Enigma, todas elas são completamente diferentes umas das outras, por conta disso, os nazistam estavam certos de que possuíam um código inquebrável.

A logística da guerra

A logística de guerra dos Alemães era simples, as mensagens eram cifradas e transmitidas via código morse por um operador de radio, do outro lado, outro Alemão com uma maquina Enigma configurava da mesma forma que a maquina usada para criptografar as mensagens, digitava as mensagens cifradas e a maquina retornava as mensagens traduzidas. Porem, para isso funcionar ele precisava saber como a maquina que criptografou as mensagens, para isso, a Alemanha nazista distribuia uma folha com as configurações da maquina enigma para um determinado mês.

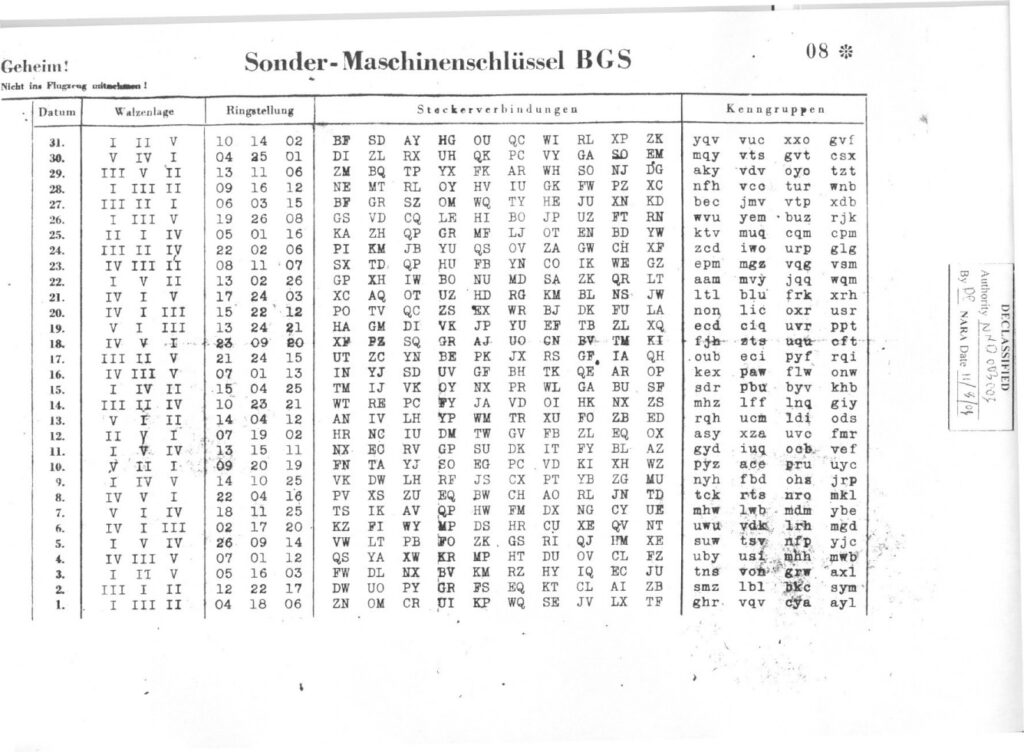
Enigma codesheet

Assim, para que qualquer um não autorizado conseguir traduzir as mensagens era necessário acesso tanto a maquina enigma, quanto esse papel com as configurações da maquina. Durante a segunda guerra os Aliados conseguiram facilmente acesso a Enigma, porem a folha era quase impossivel de se conseguir, uma vez que era facilmente destruida.

A falha dentro da Enigma

Para entendermos de fato como se deu a quebra do código enigma primeiro precisamos entender a falha da Enigma. Vamos tomar a seguinte frase criptografada pela enigma, assim como era, o texto não possui espaços:

...apcdpanlyguhdykgiponluybwlxal...

Uma falha ja conhecida da Enigma é que uma letra do texto original nunca será ela mesma no texto cifrado, ou seja, ao digitarmos a letra “A” na maquina Enigma teremos uma outra letra que irá se acender, essa letra acessa corresponde a letra do texto cifrado, porem, essa letra do texto crifrado nunca será a própria letra “A”.

Quebrando a Enigma

Vamos voltar a nossa frase criptografada pela enigma:

...apcdpanlyguhdykgiponluybwlxal...

Já se era sabido que os nazistas em sua primeira mensagem do dia transmitiram a previsão do tempo para aquele dia, logo poderíamos pressupor algumas palavras, como por exemplo “previsao do tempo”, mas tambem sabemos que uma letra do texto original nunca seria ela mesma no texto cifrado, logo poderíamos supor uma possível posição para uma parte do texto:

...apcdpanlyguhdlkgiponluybwlxal...
....previsaodotempo...

No exemplo acima, podemos ver que essa não pode ser a posição da frase “previsao do tempo”, uma vez que o p do texto cifrado esta na mesma posição do p no texto original. Assim podemos continuar com esse método até encontrarmos uma posição valida. Por exemplo, vamos tomar essa posição valida:

. a p c d p a n l y g u h d y k g i p o n l u y b w l x a l .
. x x x x x x p r e v i s a o d o t e m p o x x x x x x x x .

No contexto da guerra, supor possíveis palavras nos textos do alemães era algo relativamente fácil, mas em especial, algo que estava sempre em todas as mensagens e que foi usado amplamente para esse método de quebra foi a famosa frase “heil hitler”.
Mas como usamos essa falha para quebra o código Enigma ?

A cada manhã o código enigma era trocado, antes da Alan Turing, todas amanhãs pessoas usavam o seguinte método para quebra a cifra Enigma. Vamos primeiro simplificar como a Enigma funciona, primeiro ao pressionar uma tecla o sinal elétrico irá passa pela plugboard, depois pelos rotes, para então passar pela plugboard novamente.

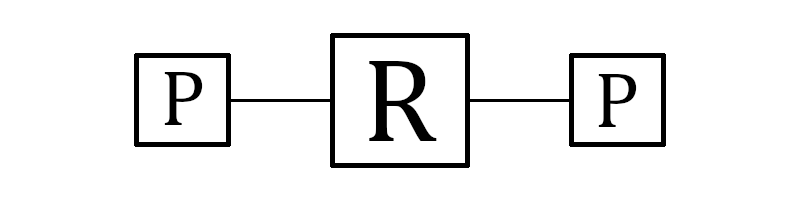
Enigma simplificada

O processo de quebra começa assumindo algo, por exemplo, a partir da código de exemplo mais acima sabemos que, quando pressionamos a letra “O” temos no fim do processo a letra “Y”, vamos supor que a letra “O” esteja conectada a letra “A” no painel plugboard, assim vamos ter:

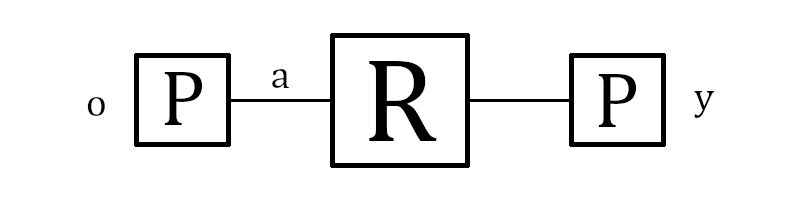
Enigma simplificada

Como é possível saber como os rotores são, uma vez que os Aliados já tinham em mãos a Enigma, escolhemos uma posição para os rotores e verificamos qual a letra que sai dos rotores quando temos a letra “A”, nesse caso vamos dizer que é a letra “K”:

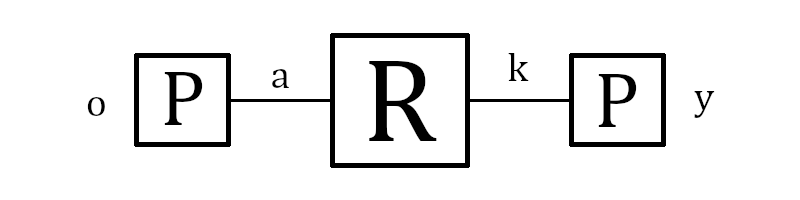
Enigma simplificada

Dessa forma podemos supor então que a letra “K” esta conectada a letra “Y” no painel plugboard. Assim, podemos continua com essa mesma logica e deduzir as letras que estão ligada no painel plugboard, vamos tomar essas saídas para a letra “O” dadas no exemplo:

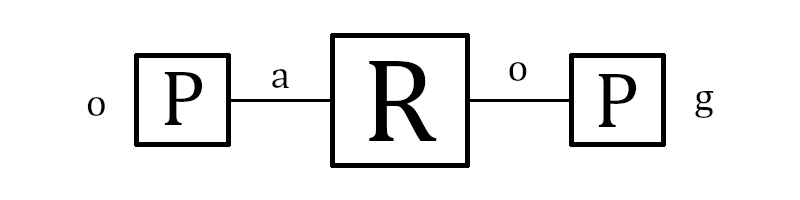
Enigma simplificada

Na segunda ocorrência da letra “O” já temos um problema, daqui temos que “O” está ligado em “A”, porem com os rotores, descobrimos que “O” está ligado em “G”, o que não é possivel, uma letra só pode ser conectada a uma única letra, assim podemos dizer que a posição dos roteres está errada, assim podemos recomeçar o processo.
A maquina de Alan Turin foi algo revolucionário para a época, porque a maquina checava essas condições, assim que chagava no mesmo problema que chegamos ela recomeçava mudando a posição dos rotores e recomeçando todo o processo. Assim a maquina parava assim que atingia uma combinação que não resultava em nenhum tipo de incongruência, quebrando perfeitamente a cifra gerada pela Enigma.

A importância histórica

A análise da máquina Enigma e a criação da computador Bombe por Alan Turing foram de extrema importância para a humanidade e para a matemática, especialmente durante a Segunda Guerra Mundial. A Enigma era uma máquina de criptografia alemã que protegia as comunicações militares, e sua quebra pelos Aliados foi uma tarefa extremamente desafiadora. Foi nesse contexto que Alan Turing, um brilhante matemático e pioneiro da computação, desempenhou um papel crucial ao liderar a equipe que buscou decifrar o código Enigma.

A criação do dispositivo mecânico que acelerou significativamente o processo de quebra do código Enigma. A Bombe usava princípios matemáticos e de lógica para testar diversas configurações possíveis dos rotores da Enigma e do plugboard. Graças ao trabalho de Turing e sua equipe, os Aliados conseguiram decifrar as comunicações criptografadas dos alemães, obtendo informações vitais sobre suas estratégias e movimentos militares. Mais adiante, maquinas como a Bombe foram aperfeiçoadas ao longo do tempo, para chegar hoje no que nos conhecemos como os computadores. O conceito de uma máquina universal de Turing, que inspirou a criação dos computadores digitais, foi fundamental para o desenvolvimento da tecnologia da informação e transformou a maneira como vivemos e trabalhamos.

Alem disso essa conquista teve um impacto direto no curso da guerra, salvando inúmeras vidas e acelerando a derrota do Eixo. A capacidade dos Aliados de interceptar e interpretar comunicações secretas alemãs proporcionou uma vantagem estratégica significativa e permitiu que tomassem decisões mais informadas nos campos de batalha. A quebra do código Enigma abriu novos caminhos na criptoanálise e na matemática aplicada. As técnicas desenvolvidas por Turing e sua equipe para decifrar o código Enigma levaram a avanços significativos na teoria dos números, álgebra abstrata e probabilidade, ampliando o conhecimento matemático e seu potencial para resolver problemas complexos.

Bibliografia

[1] CONTRIBUIDORES WIKIPEDIA. Cryptography. [S. l.], 2019. Disponível em: https://en.wikipedia.org/wiki/Cryptography. Acesso em: 19 jul. 2023.

‌[2] CHURCHHOUSE, Robert. Codes and ciphers : Julius Caesar, the Enigma, and the internet. Cambridge ; New York: Cambridge University Press, 2002-.

‌[3] ALBRECHT BEUTELSPACHER; J CHRIS FISHER. Cryptology : an introduction to the art and science of enciphering, encrypting, concealing, hiding, and safeguarding described without any arcane skullduggery but not without cunning waggery for the delectation and instruction of the general public. Washington, Dc: Mathematical Association Of America, 1994-.

‌[4] REINHARD WOBST; SHAFIR, Angelika. Cryptology unlocked. Chichester: John Wiley & Sons, 2007-.

[5] O’CONNOR, J J; ROBERTSON, E F. Alan Turing – Biography. [S. l.], 2003. Disponível em: https://mathshistory.st-andrews.ac.uk/Biographies/Turing/. Acesso em: 19 jul. 2023.

‌[6] NUMBERPHILE. 158,962,555,217,826,360,000 (Enigma Machine) – Numberphile. YouTube, 2013. Disponível em: https://www.youtube.com/watch?v=G2_Q9FoD-oQ. Acesso em: 21 jul. 2023.

‌[7] NUMBERPHILE. Flaw in the Enigma Code – Numberphile. YouTube, 2013. Disponível em: https://www.youtube.com/watch?v=V4V2bpZlqx8. Acesso em: 21 jul. 2023.

‌

‌

‌