O Teorema de Bolzano e o Método da Bisseção se destacam como ferramentas poderosas na análise e solução de equações. Neste artigo, vamos explorar esses conceitos fundamentais, aplicando-os com a ajuda da linguagem de programação Python e utilizando o Manim para criar imagens e animações que facilitam a compreensão visual dos métodos.
O Teorema de Bolzano, também conhecido como Teorema do Valor Intermediário, é um dos pilares do cálculo. Ele afirma que, se uma função contínua tem valores de sinais opostos em dois pontos de um intervalo, então ela possui pelo menos um ponto nesse intervalo onde seu valor é zero. Esse teorema é crucial para garantir a existência de raízes em equações.
Com base no Teorema de Bolzano, o Método da Bisseção é uma técnica iterativa para encontrar raízes de funções contínuas. Ele funciona dividindo repetidamente o intervalo onde a raiz está localizada e selecionando o subintervalo que contém a raiz, até que a aproximação seja suficientemente precisa. Este método é conhecido por sua simplicidade e robustez, sendo amplamente utilizado em problemas de análise numérica.
Neste artigo, não apenas descreveremos a teoria por trás desses conceitos, mas também demonstraremos como implementá-los em Python. Utilizaremos a biblioteca Manim para criar animações que ilustram o funcionamento do Método da Bisseção, tornando o aprendizado mais dinâmico.
Existência e unicidade de uma raiz em um intervalo
Teorema de Bolzano – Se \(f : [a, b] \rightarrow \mathbb{R}\), \(y = f(x)\), é uma função contínua tal que \(f(a) \cdot f(b) < 0\), então existe \(x^* \in (a, b)\) tal que \(f(x^*)=0\).
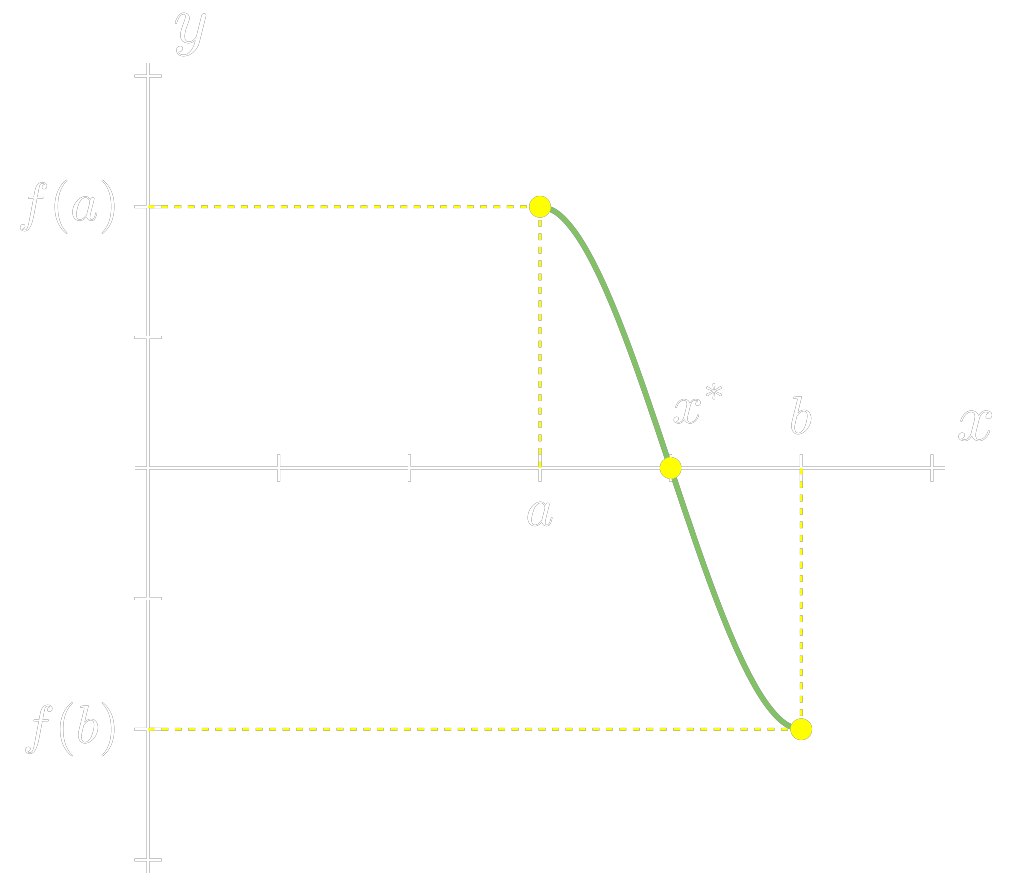
Em termos simples, o teorema de Bolzano nos diz que se uma função \(f\) troca de sinal em um intervalo, podemos garantir que existe ao menos um valor de \(x\) onde a função intersecta o eixo \(x\). Com isso podemos facilmente construir uma função para checar a existência de uma raiz em um dado intervalo:
def f(x):
return (x**3) - (12*(x**2)) + (45*x) - 52
#retorna true se houver uma raiz no intervalo
def bolzano(start,end):
if (f(start) * f(end)) < 0:
return True
else:
return False
print(bolzano(3,5))Os parâmetros da função bolzano são os pontos do intervalo que queremos analisar, dessa forma a função irá realizar a multiplicação do valor dos pontos inseridos e verificar se seu valor é negativo (menor que 0), caso seja, a função retorna o valor True (verdadeiro), caso contrario ela retorna o valor False (falso).
Podemos ainda otimizar um pouco o código da seguinte forma:
def f(x):
return (x**3) - (12*(x**2)) + (45*x) - 52
#retorna true se houver uma raiz no intervalo
def bolzano(start,end):
return (f(start) * f(end)) < 0:
print(bolzano(3,5))Essa função possui a mesma funcionalidade da anterior, porem agora estamos retornando o valor da comparação diretamente.
Outro ponto importante, é que o teorema de Bolzano garante a existência de uma raiz no intervalo, e não a unicidade, com a mesma função \(f(x) = x^3-12x^2+45x-52\) podemos ver que no intervalo \([2,6]\) o código retorna True, ou seja, existe uma raiz no intervalo, mas ao analisarmos o gráfico da função podemos ver que existem 3 raízes no intervalo:
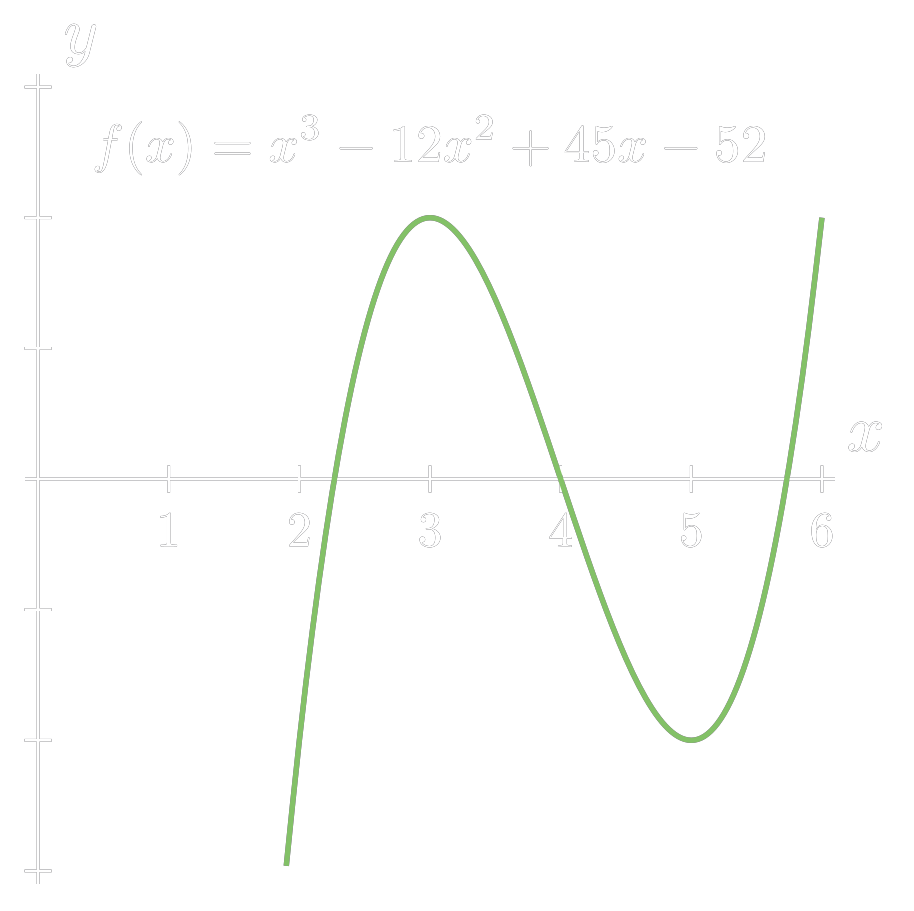
Para garantir a unicidade poderíamos usar a seguinte proposição para verificar a unicidade uma raiz em um intervalo.
Proposição – Se \(f : [a, b] \rightarrow \mathbb{R}\), \(y = f(x)\), é uma função diferenciável, \(f(a) \cdot f(b) < 0\) e \(f'(x)>0\) \(\forall x\in(a,b)\), então existe um único \(x^* \in(a,b)\) tal que \(f(x^*)=0\).
Essa proposição diz que se não houver nenhuma troca de sinal dentro do intervalo existe apenas uma raiz no intervalo, caso haja alguma raiz no intervalo. Porem esse seria um método custoso de checarmos usando Python (ou qualquer outra linguagem), pois precisaríamos checar o valor da derivada da função por todo o intervalo.
Encontrando a raiz em um intervalo
Método da bisseção
O método da bisseção consiste em dividir um intervalo, onde sabemos que existe ao menos uma raiz, em dois intervalos e analisar os dois intervalos menores, escolhemos o intervalo menor que contem a raiz, e usando o teorema de Bolzano novamente, e repetimos o processo até que um certo número de interações seja atingido e/ou um certo valor de precisa, seja alcançado. Abaixo podemos ver uma possível visualização para o Método da bisseção:
Podemos ver na visualização acima que dado um seguimento inicial dividimos ele ao meio, no ponto amarelo, todos os seguimentos marcado em azul contem a raiz da função, durante as interações escolhemos esse seguimento para fazer o mesmo processo. Dessa forma, nos aproximamos cada vez mais da raiz da função.
Uma possível aplicação para o método da bisseção segue:
interval = (3,4.5)
def f(x):
return (x**3) - (12*(x**2)) +(45*x)-52
def bisection(f,interval,N,tolerance):
i = 0
fa = f(interval[0])
a = interval[0]
b = interval[1]
while(i<N):
#ponto médio do intervalo
m = a + (b-a)/2
fm = f(m)
#checagem para condição de parada
if(fm == 0) or ((b-a)/2 < tolerance):
return m
#bissecao do novo intervalo
i += 1
if (fa * fm > 0): #bolzano
a = m
fa = fm
else:
b = m
print(bisection(f,interval,10,0.001))Nesse algoritmo temos a função bisection que recebe como parâmetro uma função que usamos para retornar os valores da função e checar pelo teorema de Bolzano, o interval uma tupla (ou array) com o intervalo para a interação, um intervalo ao qual começamos a interação, um N máximo para as interações e o parâmetro tolerance que chega o tamanho do intervalo, ao chegarmos nesse tamanho de intervalo o processo é parado.
Na função definimos uma variável i para marcar a quantidade de interações que já executamos, nesse caso inicializamos ela em 0. Em seguida definimos algumas variáveis iniciais para as interações, nesse caso definimos a e b com os valores do parâmetro interval. O loop while checamos o número de interações i com o número máximos de interações N. Dentro do loop temos 3 partes principais, primeiro definimos o ponto médio m no intervalo e o valor dele na função f, em seguida checamos se fm é igual a 0 (pois caso seja, já encontramos a raiz) ou se o tamanho do intervalo é menor do que a tolerância definida, caso alguma dessas condições seja verdadeira retornamos o valor de m.
Por último, caso o valor de m ainda não tenha sido retornado, usamos novamente o teorema de Bolzano para chegar qual dos intervalos contem a raiz, e ajustamos os calores de a e b de acordo.
Muito embora esse seja um código funcional ele possui um problema, existem certas combinações de intervalos e valores de tolerância e interações que podem resultar em nenhum valor sendo retornado, vejamos o exemplo do código acima, temos um intervalo igual a \((3,4.5)\), um número de interações igual a \(10\) e uma tolerância de \(0.001\). Como o método da bisseção sempre divide o intervalo na metade com \(n\) interações temos que o menor intervalo terá um comprimento \(c\):
\(c=\left( \frac{b-a}{2} \right)^n\)
Nesse exemplo temos um \(n = 10\), ou seja, teremos um \(c = 0.00146484375\), nessas condições, caso fm seja sempre diferente de 0, o valor de m nunca será retornado e iremos “esgotar” as interações, dessa forma a função bisection termina sua execução sem ter um valor de retorno, por isso vemos o Python retorna None.
Para contornar isso temos duas saídas, assim como sugerido em [1], podemos adicionar a seguinte linha no fim da função, fora do loop while:
raise NameError('Num. max. de iter. excedido!')Isso ira fazer o programa retornar uma mensagem de erro. Outra solução, é armazenar o valor de m, caso a função não atinja o valor exato da raiz ou a tolerância não seja atingida, podemos retornar o valor “parcial” de m:
interval = (3,4.5)
def f(x):
return (x**3) - (12*(x**2)) +(45*x)-52
def bisection(f,interval,N,tolerance):
i = 0
fa = f(interval[0])
a = interval[0]
b = interval[1]
result = 0
while(i<N):
#ponto médio do intervalo
m = a + (b-a)/2
fm = f(m)
#checagem para condição de parada
if(fm == 0) or ((b-a)/2 < tolerance):
return m
#bissecao do novo intervalo
i += 1
if (fa * fm > 0): #bolzano
a = m
fa = fm
else:
b = m
result = m
return result
print(bisection(f,interval,10,0.001))Dessa forma sempre teremos um valor retornado. Ambas as formas são funcionais e podem ser usadas conforme a necessidade.
Referências
[1] JUSTO, D. A. R.; SAUTER, E.; AZEVEDO, F. S. de; GUIDI, L. F.; KONZEN, P. H. de A. Cálculo Numérico. [S. l.: s. n.], 2020. Disponível em: https://www.ufrgs.br/reamat/CalculoNumerico/livro-py/livro-py.pdf.
